목차
1. Properties to Compare
2. 정렬 알고리즘들의 성능 비교
3. 특정 상황에서의 정렬 알고리즘 선택 기준
1. Properties to Compare
성능을 비교하기에 앞서 고려해야 할 속성들에 대해 간단히 알아보자.
① Time Complexity Comparison
- Best: 가장 효율적으로 동작할 경우의 시간 복잡도
- Average: 일반적인 경우의 시간 복잡도
- Worst: 최악의 경우의 시간 복잡도
② Auxiliary Space Complexity Comparison (보조 공간 복잡도)
알고리즘이 추가로 필요한 메모리 공간을 의미한다. 예를 들어, In-Place 알고리즘(ex. quick, heap)은 추가적인 공간이 거의 필요하지 않고 입력 데이터 자체를 사용해 정렬을 수행하는 반면, 비 In-Place 알고리즘(ex. merge)은 추가적인 메모리 공간이 필요하다.
③ Online
Input 데이터를 순차적으로 받아들이면서 정렬할 수 있는 알고리즘을 Online 정렬 알고리즘이라고 한다. 즉, 모든 input 데이터를 한 번에 받지 않고 새로운 데이터가 들어올 때마다 즉시 정렬을 처리할 수 있다. (ex. Insertion)
④ Stable
정렬 알고리즘이 안정적이라는 것은, 동일한 값을 가진 요소들의 상대적인 순서가 정렬 후에도 유지된다는 의미이다. 예를 들어, 배열 안에 4라는 값이 두 개 있을 때, 첫 번째 4와 두 번째 4는 정렬 후에도 순서가 바뀌지 않고 동일하게 유지된다.
⑤ In-Place (제자리 정렬 알고리즘)
Input 데이터 외에 추가적인 공간을 거의 사용하지 않는 알고리즘을 뜻한다. 보통 O(1) 또는 O(log n)의 추가 공간을 사용한다.
2. 정렬 알고리즘들의 성능 비교
#Bubble #Selection #Insertion #Merge #Quick #Heap
2.1. Bubble Sort
Bubble Sort는 간단하지만 효율성은 떨어지는 알고리즘이다.
1. 배열의 첫 번째 요소부터 시작하여 인접한 두 요소를 비교
2. 만약 첫 번째 요소가 두 번째 요소보다 크면, 두 요소를 교환
3. 이 과정을 배열의 끝까지 반복. 한 step이 끝나면 가장 큰 요소가 배열의 끝으로 이동하게 됨.
4. 남은 배열 부분에 대해 이 과정을 반복 (더 이상 요소 교환이 없을 때까지 반복)

function bubbleSort(arr) {
let n = arr.length;
for (let i = 0; i < n - 1; i++) {
for (let j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// 요소 교환
let temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
return arr;
}
const arr = [5, 2, 9, 1, 5, 6];
console.log(bubbleSort(arr)); // [1, 2, 5, 5, 6, 9]
① Time Complexity
Best Case는 배열이 이미 정렬된 경우이다. 이땐 한 번의 step로 종료되기 때문에 O(n)의 시간복잡도를 가진다. 하지만 대부분의 경우는 모든 요소가 골고루 섞여 있기 때문에, 여러 step에 걸쳐 모든 요소를 여러 번 비교해야 한다. Worst case는 배열이 역순으로 정렬된 경우일 것이며, 이 경우에 O(n^2)의 시간 복잡도를 가진다.
② Auxiliary Space Complexity
추가적인 공간을 사용하지 않고 입력된 배열 내에서 swapping만 이루어지므로, O(1)의 공간 복잡도를 가진다.
③ Online
Online 알고리즘이려면 정렬 중간에 새로운 데이터가 들어와도 그 즉시 처리할 수 있어야 하는데, bubble sort는 모든 데이터를 한 번에 받아서 수행해야 한다. 배열의 모든 요소를 반복적으로 비교하고 교환하며, 부분적인 데이터만으로는 정렬을 완료할 수 없기 때문에 새로운 데이터가 들어올 때마다 배열의 모든 요소를 다시 정렬해야 한다. Worst case가 O(n^2)인데, 새로운 데이터가 들어올 때마다 전체 배열을 다시 정렬해야 한다면 성능적으로 매우 비효율적일 것이다.
④ Stable
두 요소를 교환할 때, 동일한 값을 가진 요소들의 순서를 바꾸지 않기 때문에 stable하다고 볼 수 있다.
⑤ In-Place
추가적인 공간이 필요하지 않기 때문에 In-Place 알고리즘이라고 할 수 있다.
| Time Complexity | Aux. Space Complexity |
Online | Stable | In-Place | |||
| Best | Avg | Worst | |||||
| Bubble | O(n) | O(n^2) | O(n^2) | O(1) | X | O | O |
2.2. Selection Sort
Selection sort는 배열에서 가장 작거나 큰 요소를 선택해서 정렬하는 방식이다.
1. 배열의 첫 번째 요소부터 시작하여 가장 작거나 큰 요소를 찾는다
2. 찾은 가장 작은 요소를 현재 위치의 요소와 교환한다
3. 다음 위치로 이동하여 그 이후의 요소들 중에서 가장 작은 요소를 찾고 교환한다
4. 이 과정을 배열의 끝까지 반복한다

function selectionSort(arr) {
let n = arr.length;
for (let i = 0; i < n - 1; i++) {
// 최소값을 찾기 위한 인덱스
let min_idx = i;
for (let j = i + 1; j < n; j++) {
if (arr[j] < arr[min_idx]) {
min_idx = j;
}
}
// 최소값을 현재 위치로 이동
if (min_idx !== i) {
let temp = arr[i];
arr[i] = arr[min_idx];
arr[min_idx] = temp;
}
}
return arr;
}
const arr = [64, 25, 12, 22, 11];
console.log(selectionSort(arr)); // [11, 12, 22, 25, 64]
① Time Complexity
모든 case에서 모든 요소를 비교해야 하므로 best, average, worst case에서 O(n^2)의 시간 복잡도를 가진다.
② Auxiliary Space Complexity
추가적인 공간이 필요하지 않으므로 공간복잡도는 O(1)이다.
③ Online
Selection sort도 bubble sort와 마찬가지로 정렬 중간에 새로운 데이터가 들어오면 다시 처음부터 정렬해야 하므로 online 알고리즘이 아니다.
④ Stable
작은 값을 앞으로 이동시키는 과정에서 동일한 값들의 원래 순서가 바뀔 수 있으므로 stable하지 않다.
⑤ In-Place
추가적인 공간을 사용하지 않으므로 In-Place 알고리즘이다.
| Time Complexity | Aux. Space Complexity |
Online | Stable | In-Place | |||
| Best | Avg | Worst | |||||
| Selection | O(n^2) | O(n^2) | O(n^2) | O(1) | X | X | O |
2.3. Insertion Sort
Insertion sort는 간단하지만 효율적이다. 동작 방식을 간단하게 보자
1. 배열의 첫 번째 요소는 이미 정렬된 상태로 간주한다. 즉, 첫 번째 요소는 그 자체로 정렬된 부분이다.
2. 두 번째 요소부터 시작하여 배열의 모든 요소를 순차적으로 정렬된 부분에 삽입한다.
3. 현재 요소를 정렬된 부분의 적절한 위치에 삽입한다. 이를 위해, 현재 요소보다 큰 요소들의 왼쪽으로 이동시킨다.
4. 배열의 끝까지 이 과정을 반복한다.

function insertionSort(arr) {
let n = arr.length;
for (let i = 1; i < n; i++) {
let key = arr[i];
let j = i - 1;
// key보다 큰 요소들을 오른쪽으로 이동
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
return arr;
}
const arr = [12, 11, 13, 5, 6];
console.log(insertionSort(arr)); // [5, 6, 11, 12, 13]
① Time Complexity
Best case의 경우 배열이 이미 정렬되어 있을 때 교환할 필요 없이 한 step에 끝나므로 O(1)의 시간복잡도를 가진다. 하지만 골고루 섞여 있는 일반적인 경우이거나, 역순으로 배치되어 있는 최악의 경우에는 모든 요소를 비교하고 교환해야 하므로 O(n^2)의 시간 복잡도를 가진다.
② Auxiliary Space Complexity
추가적인 공간 없이 입력된 배열 안에서 모든 비교와 교환이 이루어지므로 공간복잡도는 O(1)이다. 같은 이유로 In-Place 알고리즘이라고 할 수 있다.
③ Online
정렬하고 있는 도중에 새로운 데이터가 들어와도, 현재까지의 데이터들은 정렬된 상태로 유지하면서 새로 들어온 데이터를 적절한 위치에 삽입할 수 있으므로 Online 알고리즘이라고 볼 수 있다.
④ Stable
배열의 각 요소를 이미 정렬된 부분과 비교하여 적절한 위치에 삽입하는 방식으로 동작하는데, 이 과정에서 동일한 값을 가진 요소가 있으면 순서를 바꾸지 않으므로 stable하다.
| Time Complexity | Aux. Space Complexity |
Online | Stable | In-Place | |||
| Best | Avg | Worst | |||||
| Insertion | O(n) | O(n^2) | O(n^2) | O(1) | O | O | O |
2.4. Merge Sort
Merge Sort는 divide and conquer 기법을 사용하는 효율적인 알고리즘이다.
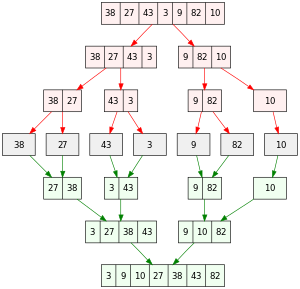
[38, 27, 43, 3, 9, 82, 10]
1. 배열을 반으로 나눈다. [38, 27, 43] [3, 9, 82, 10]
2. 다시 반으로 나눈다. [38] [27, 43] [3, 9] [82, 10]
3. length가 1이 될 때까지 나눈다. [38] [27] [43] [3] [9] [82] [10]
4. [38], [27]을 병합하여 [27, 38]로 만들고, [43], [3]을 병합하여 [3, 43]으로 만들고, ... 반복
5. [27, 38], [3, 43]을 병합하여 [3, 27, 38, 43]으로 만들고, [9, 82], [10]을 병합하여 [9, 10, 82]를 만든다
6. 이 둘을 병합하여 [3, 9, 10, 27, 38, 43, 82]를 만든다.
function mergeSort(arr) {
if (arr.length <= 1) {
return arr;
}
const mid = Math.floor(arr.length / 2);
const left = arr.slice(0, mid);
const right = arr.slice(mid);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
let result = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex++;
} else {
result.push(right[rightIndex]);
rightIndex++;
}
}
// 나머지 요소들을 결과에 추가
return result.concat(left.slice(leftIndex)).concat(right.slice(rightIndex));
}
const arr = [38, 27, 43, 3, 9, 82, 10];
console.log(mergeSort(arr)); // [3, 9, 10, 27, 38, 43, 82]
① Time Complexity
배열을 절반으로 나누고, 각 부분을 정렬한 후 다시 합친다. 분할 단계에서는 배열의 크기가 1이 될 때까지 계속 분할해야 하므로 logn번의 단계가 필요하고, 각 단계에서 배열의 요소를 비교하고 병합하는 데 O(n)의 시간이 걸리므로 어떤 상황에서든 O(nlogn)의 시간 복잡도를 가진다.
② Auxiliary Space Complexity
배열을 나누고 병합하는 과정에서 추가적인 배열 공간을 필요로 하므로 보조 공간 복잡도는 O(n)이다. 즉, In-Place 알고리즘도 아니다.
③ Online
중간에 새로운 데이터가 추가되면 전체 배열을 다시 정렬해야 하므로 online 알고리즘이 아니다.
④ Stable
동일한 값들에 대해 상대적인 위치를 유지하므로 stable하다.
| Time Complexity | Aux. Space Complexity |
Online | Stable | In-Place | |||
| Best | Avg | Worst | |||||
| Merge | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | X | O | X |
2.5. Quick Sort
Quick sort도 divide and conquer 기법을 사용한다.
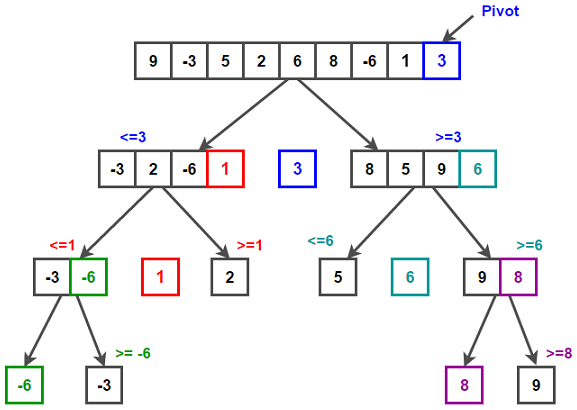
1. Pivot 선택: 배열에서 임의의 요소를 pivot으로 선택한다. 일반적으로 배열의 첫 번째 요소, 마지막 요소 또는 중간 요소이다.
2. 분할: Pivot을 기준으로 배열을 두 부분으로 나눈다. Pivot보다 작은 요소는 pivot의 왼쪽에, pivot보다 큰 요소는 pivot의 오른쪽에 위치시킨다.
3. Pivot을 제외한 왼쪽 부분과 오른쪽 부분을 재귀적으로 정렬한다.
4. 병합: 재귀 호출이 완료되면, 부분 배열들이 정렬되어 전체 배열이 정렬된다.
function quickSort(arr, low = 0, high = arr.length - 1) {
if (low < high) {
const pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
return arr;
}
function partition(arr, low, high) {
const pivot = arr[high];
let i = low - 1;
for (let j = low; j < high; j++) {
if (arr[j] < pivot) {
i++;
[arr[i], arr[j]] = [arr[j], arr[i]];
}
}
[arr[i + 1], arr[high]] = [arr[high], arr[i + 1]];
return i + 1;
}
const arr = [10, 7, 8, 9, 1, 5];
console.log(quickSort(arr)); // [1, 5, 7, 8, 9, 10]
① Time Complexity
Best case는 pivot이 배열을 균일하게 반으로 나눌 경우이다. 분할 과정은 log n번 수행되고, 각 단계에서 n개의 요소를 비교하므로, O(nlogn)의 시간 복잡도를 가진다. 일반적인 경우에 pivot이 배열을 균일하게 반으로 나누지 않더라도 비슷하게 동작하므로 O(nlogn)의 시간 복잡도를 가진다. 하지만 worst case의 경우에는 pivot이 배열에서 최솟값 또는 최댓값일 경우에 배열이 한 쪽으로만 분할된다. 이 경우에는 매 단계마다 하나의 요소만 분할되기 때문에 총 n단계가 필요하고 각 단계에서 n개의 요소를 비교하므로 O(n^2)의 시간 복잡도를 가진다.
② Auxiliary Space Complexity
Quick sort는 재귀적으로 호출되므로 재귀 호출 스택에 공간이 필요하다. Best, average case의 경우 재귀 깊이는 O(log n)입니다. Worst case의 경우에도 O(n)의 스택 공간이 필요하지만, 최악의 경우는 잘 발생하지 않으므로 quick sort의 공간 복잡도는 O(log n)이다.
③ Online
중간에 새로운 데이터가 추가되면 다시 시작해야 하므로 online 알고리즘이 아니다.
④ Stable
동일한 값들이 있을 때 pivot과 비교하고 swap되면서 순서가 바뀔 수 있으므로 stable하지 않다.
⑤ In-Place
정렬 과정에서 입력 배열 외에 추가적인 배열을 사용하지 않고, 주어진 배열 내에서 요소들을 교환하면서 정렬하기 때문에 in-place 알고리즘이라고 볼 수 있다. In-Place 알고리즘인지를 고려할 때는 재귀 호출 스택 공간은 일반적으로 고려하지 않는다.
| Time Complexity | Aux. Space Complexity |
Online | Stable | In-Place | |||
| Best | Avg | Worst | |||||
| Quick | O(nlogn) | O(nlogn) | O(n^2) | O(logn) | X | X | O |
2.6. Heap Sort
Heap sort는 완전 이진 트리의 특성을 고려한 알고리즘이다.
1. Heapify: 주어진 배열을 최대 힙(max heap) 또는 최소 힙(min heap)으로 변환한다.
2. Sort: 힙의 루트(최대 힙의 경우 가장 큰 값, 최소 힙의 경우 가장 작은 값)를 배열의 마지막 요소와 교환하고, 힙 크기를 줄여가며 힙 속성을 유지한다.
예) [12, 11, 13, 5, 6, 7]
1. 주어진 배열을 최대 힙으로 변환한다 => [13, 11, 12, 5, 6, 7]
2. 힙의 루트인 13을 배열의 마지막 요소 7과 교환한다.
3. 힙의 크기를 줄이고, 힙 속성을 유지하며 정렬한다.
4. 반복한다.

function heapSort(arr) {
let n = arr.length;
// 힙 구성
for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// 요소를 하나씩 힙에서 추출하여 정렬
for (let i = n - 1; i > 0; i--) {
// 현재 루트를 끝으로 이동
[arr[0], arr[i]] = [arr[i], arr[0]];
// 줄어든 힙 크기에서 힙 속성 유지
heapify(arr, i, 0);
}
return arr;
}
function heapify(arr, n, i) {
let largest = i;
let left = 2 * i + 1;
let right = 2 * i + 2;
// 왼쪽 자식이 루트보다 큰 경우
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// 오른쪽 자식이 현재 가장 큰 것보다 큰 경우
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// 가장 큰 값이 루트가 아닌 경우
if (largest !== i) {
[arr[i], arr[largest]] = [arr[largest], arr[i]];
// 재귀적으로 힙 속성 유지
heapify(arr, n, largest);
}
}
const arr = [12, 11, 13, 5, 6, 7];
console.log(heapSort(arr)); // [5, 6, 7, 11, 12, 13]
① Time Complexity
heapify 과정을 보자. 완전 이진 트리의 높이는 log n이며, 트리의 각 레벨에서 노드의 수는 2^i이다. heapify 함수가 호출될 때 최악의 경우 트리의 높이만큼 이동하게 된다. 즉, 힙을 구성하는 데의 시간 복잡도는 O(n)이다.
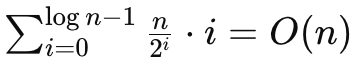
두 번째 단계는 최대 힙의 루트(가장 큰 요소)를 배열의 끝으로 이동시키고, 힙 크기를 줄여가며 힙 속성을 유지하는 것인데, heapify 함수의 시간 복잡도는 O(log n)이며 정렬 과정에서 n번 호출하므로, 총 시간 복잡도는 O(nlogn)이다.
따라서 전체 시간 복잡도는 O(n) + O(nlogn) = O(nlogn)이다.
② Auxiliary Space Complexity
Heap sort는 추가적인 공간을 사용하지 않기 때문에 공간 복잡도는 O(1)이다. 같은 이유로 In-Place 알고리즘이다.
③ Online
새로운 데이터가 추가되면 다시 처음부터 정렬해야 하므로 online 알고리즘이 아니다.
④ Stable
동일한 값을 가진 요소들이 힙 구성 과정에서 위치가 바뀔 수 있으므로 상대적인 순서가 보장되지 않는다.
| Time Complexity | Aux. Space Complexity |
Online | Stable | In-Place | |||
| Best | Avg | Worst | |||||
| Heap | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | X | X | O |
| Time Complexity | Aux. Space Complexity |
Online | Stable | In-Place | |||
| Best | Avg | Worst | |||||
| Bubble | O(n) | O(n^2) | O(n^2) | O(1) | X | O | O |
| Selection | O(n^2) | O(n^2) | O(n^2) | O(1) | X | X | O |
| Insertion | O(n) | O(n^2) | O(n^2) | O(1) | O | O | O |
| Merge | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | X | O | X |
| Quick | O(nlogn) | O(nlogn) | O(n^2) | O(log n) | X | X | O |
| Heap | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | X | X | O |
3. 특정 상황에서의 정렬 알고리즘 선택 기준
앞서 살펴본 특성들을 기반으로 상황에 맞게 적절한 알고리즘을 선택하면 된다. 예를 들어, 이미 정렬된 데이터인 경우 insertion sort가 O(n)의 시간 복잡도를 가지므로 매우 효과적일 것이다. Bubble sort도 비효율적이지만, 거의 정렬된 데이터의 경우 빠르게 동작한다. 메모리 사용이 제약된 경우에는 공간 복잡도를 고려하여 O(1)인 알고리즘을 선택하고, 메모리 사용이 크게 문제가 되지 않는 경우에는 안정적이고 효율적인 merge sort를 선택할 수 있다. 안정성이 중요한 경우에는 stable 알고리즘 중에서 선택하고, 안정성이 크게 중요하지 않는 경우에는 매우 빠른 quick sort나 메모리 사용이 적은 heap sort를 선택할 수 있다. 실시간으로 데이터 처리를 해야 하는 경우에는 online 알고리즘인 insertion sort를 사용하면 효율적일 것이다.
'CS > Data Structure, Algorithm' 카테고리의 다른 글
| [백준/Node.js] 1987 알파벳 (1) | 2024.10.13 |
|---|---|
| [백준/Node.js] 3197 백조의 호수 (0) | 2024.10.13 |
| [백준/Node.js] 17071 숨바꼭질 5 (0) | 2024.10.12 |
| [자료구조] Hash Table (8) | 2024.05.09 |
| Stack 2개로 Queue, Queue 2개로 Stack 만들기 (2) | 2024.05.07 |



